Steigung in Prozent: Unterschied zwischen den Versionen
| Zeile 90: | Zeile 90: | ||
==weiterführende Links== | ==weiterführende Links== | ||
| − | + | * [[Dreisatz#gerader_Dreisatz|Gerader Dreisatz]] | |
* [[Winkelfunktionen]] | * [[Winkelfunktionen]] | ||
* [[Vergleich Prozentsteigung - Tangens]] | * [[Vergleich Prozentsteigung - Tangens]] | ||
* [[Grad - %-Steigung|Umrechnung Grad - %-Steigung]] | * [[Grad - %-Steigung|Umrechnung Grad - %-Steigung]] | ||
Version vom 19. April 2018, 10:11 Uhr
Einführung
Neigungen kann man in Grad oder in Prozent angeben. Dabei werden flachere Dachneigungen in Prozent und höhere in Grad angegeben.
|
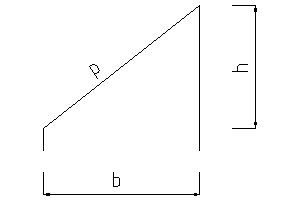
Bei der Steigungsberechnung in Prozent hat man vereinbart, dass die Breite eines rechtwinkligen (!) Dreiecks der mathematische Grundwert und die Höhe der Prozentwert der Breite ist. |
Aufgabenstellungen
Bestimme die Höhe
geg.: Breite und Prozent Steigung
ges.: Höhe
Lösung: Gesucht ist der Prozentwert, der sich mathematisch berechnet aus P = (G*p)/100. Wie oben beschrieben ist aber der Grundwert b, p die Prozentsteigung und die Höhe h der Prozentwert. Also gilt
denn, wenn man die Aufgabe als geraden Dreisatz aufstellt, gilt
| % | m | |
| 100% | <=> | Breite b |
| p% | <=> | Höhe h |
Bestimme das Breitenmaß
geg.: Höhe und Prozent Steigung
ges.: Breite
Lösung: Gesucht ist der Grundwert, der sich mathematisch berechnet aus G = (P* 100)/p. Wie oben beschrieben ist aber der Grundwert b, p die Prozentsteigung und die Höhe h der Prozentwert. Also gilt
denn, wenn man die Aufgabe als geraden Dreisatz aufstellt, gilt
| % | m | |
| p% | <=> | Höhe h |
| 100% | <=> | Breite b |
Bestimme die Steigung in Prozent
geg.: Breite und Höhe
ges.: Prozentsteigung
Lösung: Gesucht ist der Prozentsatz, der sich mathematisch berechnet aus p = (P* 100)/G. Wie oben beschrieben ist aber der Grundwert b, p die Prozentsteigung und die Höhe h der Prozentwert. Also gilt
Denn, wenn man die Aufgabe als geraden Dreisatz aufstellt, gilt
| m | % | |
| Breite b | <=> | 100% |
| Höhe h | <=> | p% |