Anwendung der Winkelfunktion/Pythagoras
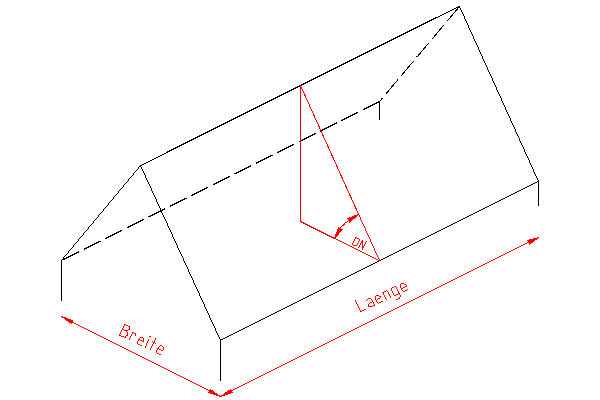
Dachfläche des Satteldaches gleicher Dachneigung
geg.:Länge, Breite und Dachneigung des Satteldaches gleicher Dachneigung
ges.:Dachfläche
Lösungsweg
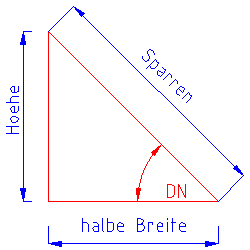
Zur Berechnung der Dachfläche des oben abgebildeten Satteldaches gleicher Dachneigung muss die Sparrenlänge ermittelt werden. Dazu kann man in dem rechts erneut abgebildeten Dreieck der Reihe nach:
- mit der Winkelfunktion die Höhe des Daches (Gegenkathete)
- mit dem Lehrsatz des Pythagoras die Sparrenlänge
berechnen.
Alternativ lässt sich die Sparrenlänge auch mit der Cosinus-Funktion ermitteln.
Beispiel
geg.:
Länge: 14.30 m
Breite: 8.24 m
Dachneigung: 42 Grad
Lösung
1. Gegenkathete im Dreieck (Dachhöhe)
Dachhöhe = 4.12 m * tan 42 = 3.71 m
2. Hypotenuse im Dreieck (Sparrenlänge)
(3.71m)² + (4.12m)² = 30.74 m
Wurzel aus 30.74 m ist 5.54 m
3. Dachfläche (Rechteck)
Länge * Sparrenlänge = 5.54m * 14.30 m = 79.22 m²
Da beide Dachflächen gleich groß sind (gleiche Dachneigung), beträgt die Gesamtfläche:
2 * 79.22 m² = 158.44 m²
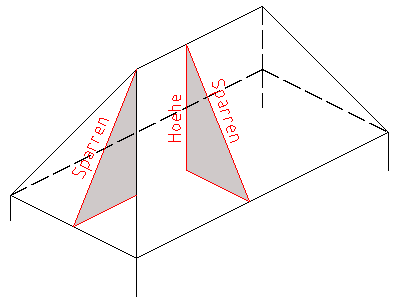
Dachfläche des Walmdaches gleicher Dachneigung
geg.: Länge, Breite und Dachneigung eines Walmdaches gleicher Dachneigung
ges.: die Dachfläche
Anmerkung
Die Sparren der Walme und der trapezförmigen Dachflächen sind gleich lang.
Lösungsweg:
1. Die Sparrenlänge wird genauso berechnet wie beim Satteldach gleicher Dachneigung.
2. Die weiteren Berechnungen erfolgen gemäß den Berechnungen für ein Walmdach (gleiche Dachneigung).
Beispiel:
Länge: 14.60 m
Breite: 9.12 m
Dachneigung: 47°
Der erste Teil der Rechnung wie beim Satteldach gleicher Dachneigung
1. Dachhöhe (Gegenkathete)
4.56 m * tan 47° = 4.89 m
2. Sparrenlänge (Hypotenuse)
(4.89 m)² + (4.56 m)² = 44.71 m²
Wurzel(44.71 m²) = 6.69 m
Siehe Walmdach (gleiche Dachneigung) für die weiteren Schritte.
3. Firstlänge
First = 14.60 m - 9.12 m = 5.48 m
4. Trapezförmige Flächen
A = (14.60 m + 5.48 m)* 6.69m/2 = 67.17 m²
5. Dreieckige Walmflächen
A = (9.12 m * 6.69 m) / 2 = 30.51 m²
6. Gesamtfläche
Da jede Fläche zweimal vorkommt:
2 * 67.17 m² + 2 * 30.51 m² = 195.36 m²